17. 统计项目一览
对n个数据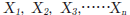 ,以下说明各种不同的统计值的求法和概要。
,以下说明各种不同的统计值的求法和概要。
| 统计项目 | 计算公式及说明 |
|---|---|
|
平均(算术平均数) |
平均又叫做算术平均数,可用以下的公式求得。 通常,只说平均的情况,就表示算术平均数。需要注意的是在含有极端的异常值、分布失真的情况下代表性会变弱。 |
|
几何平均数(幾何平均) |
几何平均数又叫几何平均,可用以下的公式求得。 在计算成长率和恶化率等“率”的平均时用到。需要注意的是无法处理负数。 |
|
调和平均数 |
调和平均数可用以下的公式求得。 需要注意的是无法使用含有0的数据。 |
|
平方平均数 |
平方平均数可用以下公式求得。 |
|
加权平均 |
各数据
|
|
中位数(Median) |
中位数是把各数据从小到大排列时在中央位置的值。数据的个数为偶数时,取离中央最近的两个数据的平均数。(中位数)是受异常值和分布失真的影响小的代表值。 |
|
众数( Mode) |
众数是考虑各数据的频率分布的情况,频率最高(出现次数最多)的数据的值。 |
|
范围(Range) |
范围是用数据的最大值中减去最小值的差,可用以下的公式求得。 |
|
离均差 |
用各数据减平均数的的差,可用以下的公式求得。 是表示各个数据与平均数距离多远的指标。 |
|
离均差平方和 |
是离均差的平方的总和,可用以下的公式求得。 是表示数据全体的分散程度的指标。由于各离均差有正负之分单纯求和会变成零,所以求平方之后和。 |
|
样本方差 |
标本方差是用离均差平方和除以标本数n的值,可用以下的公式求得。 是一个表示数据全体的分散程度的2次方的指标。样本分散的“样本”表示对某个 总体进行抽样后对于样本(或标本)的方差。因此,在处理总体中全部数据的情况下(样本=总体),“样本”就不必要了。对于样本方差, 作为总体方差(Population Variance)的估计量(使用)下述的无偏方差更好。 |
|
样本标准差 |
样本标准差是取样本方差的平方根之后的值,可用以下的公式求得。 是一个表示数据全体的分散程度的指标。与样本方差一样,“样本”表示被(从总体中)抽样。作为总体标准差(Population Standard Deviation)的估计量(使用)下述的无偏标准差更好。 |
|
无偏方差 |
无偏方差,是把偏差的平方和处以
在此 |
|
无偏标准差 |
无偏标准差是无偏方差的平方根,可用以下的公式求得。 作为总体标准差的估计量,比样本标准差更好。 |
|
标准分数 |
某个数据X的标准分数可以用以下的公式求得。 标准分数,是表示数据在总体中占据的大体位置的无量纲量。数据与总体平均相等时作为50,与其(总体平均)偏离很大时的分散程度作为10。 |
|
正态分布 |
正态分布呈吊钟形状,作为偶然性支配现象的总体分布(的一种),最常被使用, 可以用以下的公式求得。 ( μ表示平均,σ表示标准差) 正态分布用 N(μ, σ)表示。标准正态分布 N(0, 1)的计算值可以在添附的正态分布表中找出。 |
|
方差的加法定理 |
在变量
的关系,所有的
据此,以下的公式也成立。 这表示在组合设计有独立的分散的数据时,在单纯将分散相加的最差状态设计法中过有多预计(分散)边缘的可能性。比如,把2个有相同离均差的部件组合后,(可知)标准差是单体的2的平方根倍(1.414倍),而不是单体的标准差的2倍。 |
