26. Three-phase alternating current circuit and Balanced three-phase circuit
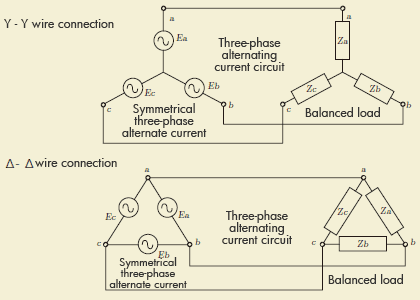
The three-phase alternating current is called the symmetrical three-phase alternate current that meets the condition of the three-phase alternating current which will be explained later. In other words, the conditions are (1)The electro motive force of the three phase are same, (2)The frequency of the three phase are same and (3)The phase differences of the respective three-phase are all in the relation with 2/3π. When these three conditions are established, the vector sum of the electromotive force of the three-phase circuit (instantaneous value) becomes 0(0). In general, it means the symmetrical three-phase alternate current circuit when we say the three-phase alternating current circuit.
| Balanced three-phase circuit |
|---|
|
Those loads are called “Balanced load” when each load of the three-phase alternating current are equal. In addition, it is called as “Balanced three-phase circuit” when the power source is symmetrical three-phase alternate current and the load is balanced load. There are several wire connection methods like Y-Y wire connection and δ-δ wire connection shown in the figures below.
|
| Relation between current and voltage in Y-Y wire connection |
|
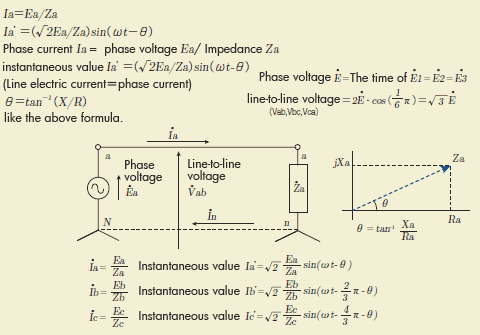
To calculate the current and voltage of the three-phase alternating current circuit, it can be done by calculating single phase alternating current circuit by breaking into a single phase circuit. Here the three-phase alternating current is assumed as the balanced three-phase alternating current. Then, since the phase differences of current and voltage between each phase are same, relation between current, voltage and a phase difference can be determined by following formulas. Ia=Ea/Za Ia’=(Root2Ea/Za)sin(Omega*t-theta) phase current Ia= phase voltage Ea/impedance Za instantaneous value Ia’=(Root2Ea/Za)sin(omega*t-theta) (Line electric current=phase current) Theta=tan-1 (X/R) Where “Theta” is a phase difference.
|
| Phase sequence of three-phase alternating current |
|
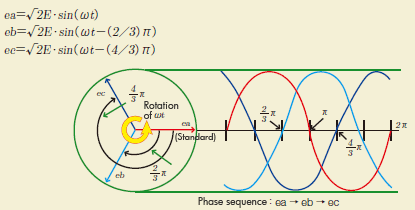
It is called the 1 phase, 2 phase, 3 phase or a phase, b phase, c phase in order of generating the electromotive force. The electromotive force of each phase of the three-phase alternating current (instantaneous value) can be expressed by the following formula.
|
| Relation between current and voltage in δ-δ wire connection |
|
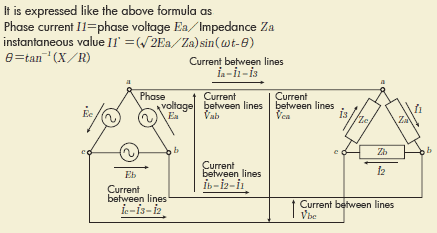
To calculate the current and voltage of the three-phase alternating current circuit, it can be done by calculating single phase alternating current circuit by breaking into a single phase circuit. Here the three-phase alternating current is assumed as the balanced three-phase alternating current. Then, since the phase differences of current and voltage between each phase are same, relation between current, voltage and a phase difference can be determined by following formulas. Phase current I1=phase voltage Ea/impedance Za instantaneous value I1’=(Root2Ea/Za)sin(omega*t-theta) (Line electric current=phase current) Theta=tan-1 (X/R) Where “Theta” is a phase difference.
|